Limite e continuidade

Palavras chave: aproximação, comportamento assintótico, limite, número, sucessão, Teorema Fundamental do Cálculo Integral (caso polinomial)

Sinta-se bem vind@ a me apontar algum defeito que você encontre no texto.

Limite é um dos assuntos centrais da Matemática em seu ofício de modelar dados para outras disciplinas. Um matemático e professor de Matemática, R. Courant, dizia que "limite é o limiar da Matemática superior" querendo dizer que quando se passava da Matemática elementar para a Matemática superior, necessariamente se havia de passar pela porta, limiar, chamada "limite". O seu primeiro uso na Matemática superior é a construção dos números reais que representam um salto significativo em relação aos outros números, naturais, inteiros e racionais.
Um número real é um limite e isto pode ser construído de diversas maneiras, eu vou lhe mostrar que um número real é o limite de sucessão de números racionais e desta forma vou completar o quadro dos números até este ponto:

O conjunto dos números naturais é o fundamento da teoria dos números e é considerado com sua propriedades sem discussão;
Com os naturais construímos os inteiros, eles vieram muito depois no processo cultural com que a Humanidade criou a Matemática, houve tempo em que se olhavam para os números negativos como uma invenção esquisita;
Com os inteiros construímos os racionais, ainda hoje se dividem as frações entre "próprias" e "impróprias" revelando o preconceito com que estes números eram vistos. Mas os números racionais já trazem alguma dificuldade com a qual nos habituamos a um ponto de nem mesmo observá-la, é a equivalência entre frações: 3, 6/2, 9/3, 12/4, ... 360/120, são algumas das representações do mesmo número e isto não nos molesta nem um pouco: cada número racional é uma classe de equivalência de frações.
E agora vem um salto significativo, os números reais que completam "os buracos" que os racionais deixam na reta... existe uma infinidade de números racionais numa vizinhança de qualquer número real. Os números reais são limites de sucessões de números racionais.

Eu já falei em aula dos números reais e para isto mencionei as descobertas de Arquimedes que já sabia da existência de "quantidade incomensuráveis" - quantidades que não podiam ser medidas e marcou a posição na história com a constante de Arquimes, o número "pi".
Esta descoberta de Arquimedes foi sensacional porque esta constante mede a proporção em que se encontram perímetro e diâmetro num círculo qualquer. Ora, na época de Arquimedes os objetos círculares não eram nada comuns como hoje são para nós que temos uma variedade muito grande de objetos circulares, discos, rodas a nossa volta e poderiamos facilmente compreender que perímetro e diâmetro se encontram numa proporção constante.
Eu não sei como Arquimedes chegou a esta complicada conclusão (é uma questão histórica interessante que você sem dúvida deve ter a curiosidade de pesquisar - depois me conte...).
A forma como poderiamos chegar hoje consistiria em fazer uma estatística medindo objetos circulares e seus diâmetro para verificar a constante de proporcionalidade. Se você fizer isto vai se supreender com os resultados díspares, porque a trena escorrega na borda dos discos... mas com paciência vai concluir que fica próximo de 3.
O que me interessa aqui é discutir este conceito: próximo, a aproximação que é justificada pelo conceito delimite.
Com trena dificilmente conseguiriamos chegar perto dos valores populares para "pi", 3.1415...
Seu digitar no meu computador:

tarcisio@cap01:~/uni$ pi 100

O resultado vai ser

3.141592653589793238462643383279502884197169399375105820974944592307816406286208998628034825342117067

consegui esta resposta, porque solicitei que um programa, instalado na minha máquina, me fornecesse a constante de Arquimedes com 100 casas decimais. E se você tiver Linux instalado pode se divertir enchendo telas e mais telas com as casas decimais do "pi" e assim superar a aproximação desta constante que preenche as paredes de uma sala de um museu em Paris, mas , mesmo que você preencha algumas centenas de telas com as casas decimais da constante de Arquimedes, ainda assim, será apenas uma aproximação que você terá conseguido.
É muito difícil de obter esta constante com meios elementares, por exemplo com um programa que calcule o perímetro de um polígono regular convexo inscrito no círculo unitário e divida este número pelo dobro do raio (diâmetro). O círculo unitário com um polígono regular convexo de 10 lados inscrito,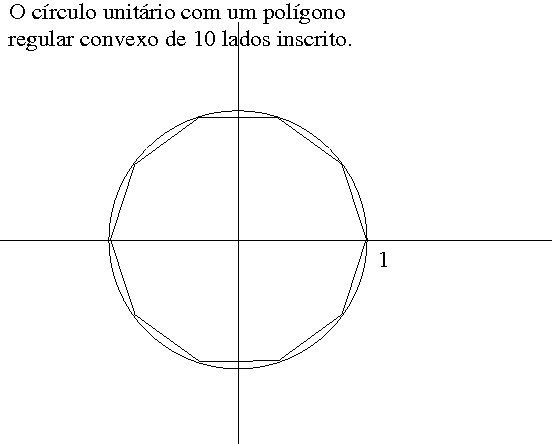

polígono regular convexo inscrito no círculo

é o que você pode ver na figura ao lado. É fácil escrever um programinha para calcular o perímetro, mas com uma falsidade interna, porque vai usar as funções trigonométricas para calcular o comprimento dos lados. Embora epistemologicamente falso ele serve para mostrar algumas casas decimais da constante de Arquimedes:
3
3.1
3.14
3.141
.............
e você tem um exemplo de uma sucessão de medidas lhe dizendo que o quociente entre perímetro e diãmetro de um objeto circular qualquer parece ser maior do que 3.
Não é necessário usar círculos com raios diferentes... por semelhança de triângulos, aplicada aos polígonos regulares, você pode chegar à conclusão de que resultado não depende do raio do círculo.
Aqui você o método científico generalizando o resultado para qualquer círculo ou disco.

Sucessões

Tudo que se pode tirar de interessante no texto acima é que usamos sucessões para produzir experimentos. Elas são usadas de forma empírica em levantamentos estatísticos - amostragens - e eu mostrei um exemplo de aplicação empírica aqui com o "programa" que citei.
Deixe-me apresentar-lhe a notação que usamos para as sucessões que são funções definidas no conjunto dos números naturais mas para as quais usamos uma notação muito particular:
Notação: Se s representa uma sucessão então o seu valor no número natural n é indicado como s_n e não com a forma habitual para funções: s(n).
Há algumas outras "liberdades" que habitualmente tomamos relativamente às sucessões, por exemplo, sem o menor pudor escrevemos a sucessão
s_n = 1/n
sem mencionarmos, como deveriamos, que n > 0.
Um dos objetivos deste texto é o de explicar este deslize habitual.
Você vai ver que este "deslize" ocorre porque os números reais também se classificam em classes de equivalência. As sucessões se classificam em classes de equivalência o que torna irrelevante alguns pontos particulares da mesma - o que interessa mesmo é o que vem depois...
O que realmente interessa numa sucessão é o seu comportamento assintótico ou o limite que ela define: um número real.

Classificando as sucessões

O meu objetivo aqui é representar números com as sucessões, mas vou usar uma linguagem experimental com o intuito de tornar o assunto mais motivador.
Para começar, "experimentos" são tentativas de modelar a realidade e muitas vezes a "realidade" é agressiva frente aos nossos resultados (aqueles que gostariamos de obter).
Por exemplo, pense num físico grego há alguns milênios tentando compreender o que se passa com um pêndulo, quer dizer, com a força de gravidade.
Depois de algumas tentativas amarrando uma pedra em algum ponto para repetir o experimento do pêndulo, ele consegue algumas melhoras evitando o atrito com o ponto de apoio mas sempre o pêndulo parando depois de algum tempo.
Neste momento ele descobre que também tem a resistência do ar, mesmo depois de transferir o experimento para dentro de uma prédio (ainda tem ar no prédio).
Então o físico grego faz uma hipótese: se não houvesse nem ar, e nem atrito no ponto de apoio, o pêndulo seguiria indefinidamente no seu vai-e-vem.
Neste momento o cientísta criou uma situação abstrata que lhe permitiu emitir uma lei geral que vale no Universo: a Terra é um pêndulo cujo suporte é o Sol e ela não para nunca...(nunca devemos dizer "nunca"). O físico grego precisou de formular o problema de modo abstrato para compreender as leis do Universo finalmente melhor descrita por Newon: existe uma força em que matéria atrae matéria .....
Então ele registra isto dizendo que a sucessão de suas medidas seriam:
10, -10, 10, -10, ....

em que as reticêncis tem um significado, fazem parte da notação, e o "10" é a distância com que em ele deu energia potencial ao sistema.
Depois de algum tempo ele melhora a notação escrevendo
s_n = (-1)ⁿ*10
não esquecendo que n é um número natural, portanto
n = 0, 1, ...
Com isto ele "corrigiu" a realidade e os resultados que ela havia antes obtido que seriam:
t_n = (-1)ⁿ*(10/n)
Tenho aqui dois tipos de sucessão e escrevi uma etiqueta classificatória ao lado de cada uma:

s_n = (-1)ⁿ*10
uma sucessão limitada;
t_n = (-1)ⁿ*(10/n) uma sucessão que tem limite zero;

Observe que a sucessão que tem limite zero, também élimitada. A questão 2 da terceira lista faz com que você pense neste conceitos, e questão 3 vai induzí-@ à formulação dos conceitos.
Aqui há uma evidente dificuldade linguística que se tornou parte da conceituação matemática sendo portanto muito difícil de corrigir, é melhor nos acostumarmos à imperfeição linguística. Até mesmo porque as nossas linguas naturais tem "limites" muito severos - não temos palavras suficientes para todos os conceitos, sempre temos mais de um conceito associado a um único vocábulo.
E na própria frase com que comentei o problema, involuntariamente, usei o vocábulo "limite" com mais um significado...
O gráfico seguinte sugere

sucessão ilimitada

uma sucessão que não tem cota (nem superior nem inferior), portanto é ilimitada:

Os pontos da sucessão, cada mais ficam dispersos no plano.
No gráfico abaixo a sugestão é de que os pontos da sucessão se mantem entre duas cotas (superior e inferior). duas cotas: superior e inferior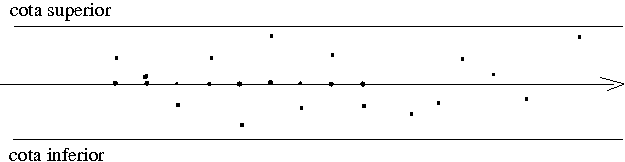

Finalmente, diferente dos dois outros, podemos ver uma sucessão representando as fotos das posições do peso do pêndulo a cada unidade inteira de minuto... o movimento amortecido do peso do pêndulo. sucessão que tende a zero então o exemplo sugere que a sucessão tende a zero (ou tem limite zero).
Eu usei a palavra sugestão porque gráficos ou programas de computador nada provam, são exemplos que no máximo conseguem retratar uma parte finita do fenômeno. O pêndulo para, porque na verdade ele vai alterando o seu movimentos com pequenos saltos devido ao atrito no suporte. Por melhor que seja feita a lubrificação no suporte as peças dão pequenos saltos consumindo a energia cinética do pêndulo, tranformando energia cinética em calor. Finalmente, um último salto, e o pêndulo para.
Não tem nenhuma semelhança com a expressão matemática que eu usei acima ao descrever o péndulo que nunca se anula. Sobre a expressão matemática podemos dizer que, para qualquer erro escolhido como cota superior (positiva) ou inferior (negativa), os valores da sucessão terminam entrando na faixa delimitada por estas cotas.
É isto que está expresso no item (c) da questão 03 da lista três.

Classificação das sucessões de números racionais

Eu não vou construir os números reais cuidadosamente aqui. Interessa-me apenas passar-lhe uma informação genérica sobre estes números que lhe permita compreender e fazer as operações fundamentais com os reais e seu uso nas funções. As funções são o objeto central do Cálculo e duas operações fundamentais que podemos fazer com elas: derivação e integração.
Em estudos mais avançados de Matemática esta construção dos números reais é retomada de forma mais completa e não pode ser o meu objetivo aqui.
Mas uma primeira mensagem fundamental lhe foi passada: os números reais são sucessões de números racionais. Mas há pelo menos dois tipos (classes) de sucessões que eu já ilustrei graficamente acima:

sucessões divergentes para as quais não podemos encontrar nenhum comportamento assintótico;
e sucessões que convergem para zero definindo a situação de energia zero do pêndulo: o número zero.

As sucessões "caóticas", que parecem não ter nenhum comportamento previsível, também são importante e têm suas aplicações, mas não aqui para nós, então vou desprezá-las no Curso de Cálculo. Quando você sentir necessidade delas estará precisando de Matemática mais pesada!
Interessam-me, agora, nesta disciplina, as sucessões que vou classificar como convergentes (têm limite) e que vão representar algum número real.
Como estratégia para chegar rapidamente em um pequena teoria, eu vou começar discutindo uma classe especial das sucessões: as sucessões que convergem para zero (elas definem o número zero).

As sucessões que convergem para zero

As questões 02 e 03 lidam com este conceito comparando algumas sucessões para conduzí-l@ a ver quais são as sucessões que convergem para zero. Elas são tão importante que vão servir de base para definir as outras...
É, o zero é um conceito importante!
Uma das sentenças, na questão 03 serve para definir sucessão que converge para zero. Nela surge uma letra grega que é sempre usada para representar pequenos erros, "epsilon".
Quando calculamos, aproximadamente, e usando a concepção geométrica, a integral da funçao f(x) = x² discutimos o comportamento das sucessões:

s = s_n = 1/n;
t = t_n = 1/(n²);

e eu observei que era diferente s/t ou t/s.
Aqui temos alguma novidade! Operações com sucessões.
No Ensino Médio você se acostumou com a idéia de que era possível fazer operações com números. Agora você vai extender este processo e fazer operações com funções.
Eu posso dividir as sucessões s e t uma pela outra com resultados muito diferentes.
Antes de mais nada vou responder a uma pergunta que você pode estar se fazendo: e o que fazer com n=0 nesta divisão? Dê-me um tempo, no final deste texto eu vou retorno a esta questão, por enquanto despreze o n = 0, comece com o 1. Afinal você já escutou falar que o conjunto dos números naturais começa com 1...

s/t é a sucessão n, dos números naturais, e cresce além de qualquer cota superior - é uma sucessão divergente;
t/s é s, converge para zero;
As duas sucessões convergem para zero e isto mostra que mesmo dentro da classe das sucessões que convergem para zero há sucessões com comportamento fundamentalmente diferente.

Dizemos que t converge mais rapidamente para zero do s;
Bom, eu coloquei uma lupa sobre a classe das sucessões que convergem para zero, que está definida na questão 03-c)

Deixe-me criar uma imagem geométrica simples para as sucessões que convergem para zero, a classe das sucessões que convergem para zero, a figura abaixo,
Nesta última figura eu tentei (uma sugestão...) lhe mostrar que há diferentes tipos de sucessões que convergem para zero,

uma delas é positiva (tente identificar qual).

Outra é negativa, descubra qual.

Uma terceira oscila, ora é positiva ora é negativa, e já observamos que é uma sucessão deste tipo que modela o comportamento do pêndulo dentro do ambiente Terra... (diferente do pêndulo no sistema solar).

Aqui você já pode identificar uma solução para um dos problemas da nossa teoria, aventado na primeira aula, se não me engano: e o zero é positivo? é negativo?
Ora o zero representa o caso do pêndulo e oscila entre postivo e negativo, mas pode ser positivo ou negativo.
Vou terminar esta exposição com uma observação final: talvez a última figura @ ajude a entender o que são sucessões que convergem para zero, ela é a classe das sucessões que formam um feixpersonlig e em volta do eixo OX.
Mas esta idéia é inútil se você for escrever um programa, a única saída é usar a expressão que se encontra no item (c) da questão 03.
A mensagem que desejo lhe passar é que noções intuítivas ou geométricas são interessantes para nos conduzirem a entender melhor os conceitos, mas se não dominarmos a forma abstrata e formal de representá-los ficamos abaixo do limiar do conhecimento...
É preciso ir mais fundo!

O deslize de notação
Olhe para o gráfico que representa a classe do zero.
Observei que distintos tipos de experimentos podem encontrar uma formulação como um elemento desta classe, um deles o pêndulo em ambiente Terra. Outro poderia ser a medição, por um observador, da quantidade luz que chega até a sua nave que se encontra navegando na direção de Plutão (agora reduzido a um corpo celeste de categoria 3...) e observa que é do tipo 1/(n²) é do tipo inverso do quadrado da distância até a fonte de luz - o Sol. Vale se estiver longe do Sol, se estiver muito perto do Sol (quando n=0) não é possível medir com os instrumentos que fabricamos na Terra... mas também esta medida não interessa, nada poderá ser feito de interessante com ela, basta-nos saber que é muito grande!
Este exemplo mostra que não nos interessa nesta sucessão o valor quando n = 0, e nem certamente quando n = 1, 2, 3, ....ou talvez nem ainda quando n = 1000000. Se n representar segundos de distância do Sol na velocidade com que conseguimos trafegar no Universo, os primeiros valores de n são irrelevantes. Quer dizer, nesta sucessão o interessa começa com valores altos de n, os primeiros termos não nos interessam.
Isto justifica, rapidamente, superficialmente, o que disse anteriormente: não nos interessam alguns dos primeiros valores de uma sucessão, eles podem ter expressões ilegais (simplesmente vamos recusá-las) e passamos aquelas que são legais que representam o comportamento da sucessão.
Sei que esta explicação não é completa, aceite por enquanto... (eu vou repetir este pedido com muita frequência, mas eu sei que algumas das nebulosidades que eu for deixando para traz irão se condensar por si próprias, apenas espero que você não aceite tão facilmente!)
Primeira versão do Teorema Fundamental do Cálculo

Referências sobre Cálculo
Se você fizer uma busca na Internet irá encontra diversas páginas sobre Cálculo, tente Teorema Fundamental do Cálculo. Eu encontrei esta que me parece interessante de sugerir. Não fique apenas nela, e não se intimide com as diferenças de exposição das páginas que você visitar com as minhas. Aceite a diversidade de opiniões e de exposição!